|
���ցA�@��lj��A�t���C�g�X�P�W���[���ύX�A�����H�����ɑΉ� ���o: ERI Technical Bulletin Release, September 1998
|
�@�@�@
|
�@�@�{���e�̒��쌠�͕M�҂Ɗ�����Њ������������ɂ���܂��B�����A�]�ڂ��邱�Ƃ��ւ��܂��B
| �{��@�́A�V����`(�V�����j�A������`�i�������j�A�Ԋ���`�i��茧�j�A������`�i�R�`���j �ȂNJ֘A���鎩���̂���̋�`���ӑ��������Ɩ��̂Ȃ��Ŏg���Ă���܂��B |
�@��^�@�̗����������`�A�P���̗��������̑�����`�A�^�p���Ԃ̒�����`�A���ӂɏZ���n�̓y�n���p��������`�A��r�I�É��Ȓn��ɗ��n�����`�A�a�@�E�w�Z���̌����{�݂���`���ӂɗ��n����n��ł́A�q��@�����ɂ���Q�E����������������B
�@�����̔�Q�E���ɑ��čs�����K�ȑ���u���邽�߂ɂ́A��`���Ӓn��ɂ�����q��@�����̌�����o���邾�����m�ɔc�����A����ɏ����̊����H�����A���̕ύX�i���ցj�A�g�p�@�ށi�@��j�̕ύX�ɂ��q��@�����̏̕ω���I�m�ɗ\�����Ȃ���Ȃ�Ȃ��B
�@�{��@�͂����̗v���ɓ����邽�߁A�ŐV�̑���Z�p�A�R���s���[�^�Z�p���𑍍����ĊJ���������̂ł���B
�@���̎�@�́A��`���Ӓn��ɂ�����q��@�������x���̑�K�͎��Ԓ����i�������蓙�̒����j�̎��{����A���݂̍q��@�������x���̍L�������������WECPNL�R���^�[�̍쐬�A����ɂ͎����f�[�^�ɗ��t����ꂽ������WECPNL�R���^�[�̗\�������܂ł��I�ɍs�����̂ł���B
�@�����ł͖{��@�̓K�p�Č����A���{�C�n��ɂ�������{�̑����ł�����V����`�i�����`�j�ɂ�����1995�N�x�Ɋ����������������{������������������B
�@�{�����́A�����H��2000m����2500m�ւ̉����ɔ����A�����H�����A���ցA�@��ύX���ɂ��q��@�������x���̌���̎��ԁA�ω���c������ƂƂ��ɁA�����z�肳��鑛�����x���̔c����ړI�Ƃ��Ď��{���ꂽ�B���̂���2500m�����H���p�O�̎��Ԓ����Ƃ���1995�N�x�ɁA���p��̎��Ԓ����Ƃ���1997�N�x�ɂ��ꂼ����{�����B
�@�Ȃ��A�V����`�ɂ�����q��@�̗������A�����R���^�[���ɂ��Č��\����Ă�����u�V����`���Ӎq��@�����������v�i�����V�N�x�A�V�����E�V���s�ϑ��A���������������{�j���f�[�^���Q�l�����Ƃ��ĂQ�D�Ɏ����B
�@�܂��A��ʓI�Ȑ��l�f�[�^�̕�Ԏ�@���A�q��@�����\���ɓK�p����ꍇ�ɐ�������_���ȉ��ɐ�������B
�@��ʓI�ɁA�L���̕����̒����n�_�ɂ���������l�����ƂɁA�C�ӂ̒n�_�ɂ�����l�𐄒肷�邽�߂̎�@�Ƃ��āA�������Ԗ@���p������B�����ŕ�Ԃ̈Ӗ��́A�Ԃ�₤���ƂɗR�����Ă���B
�@��Ԗ@��p���邱�Ƃɂ��A�C�ӂ̒n�_�ɂ����鑛�����x����������A���ʂƂ��Ď��Ӓn��S�̂̑������x��������ł��邱�ƂɂȂ�B
�@���̕�Ԗ@�ɂ́A�]�����炢�����̕��@����Ă���Ă���B�L���Ȃ��̂Ƃ��ẮA���z����Ԗ@�A�ׂ����Ԗ@�y�уX�v���C����Ԗ@������B������Ԗ@�̎�@�Ƃ��Ă̓����́A�n���I�ɗ��U���������̎����l�̈ʒu�ƒl�̑��݊W����C�ӂ̒n�_�̒l�𐄒肷�邱�Ƃɂ���B
�@��1-1�͍ł���ʓI�Ɏg���Ă���u�ׂ����Ԗ@�v�������Ă���B
�@ �Q
�@ �b �������i�s����p�E�b���j�^���i�s����p�j ........................................��1-1
�������A
�Q
�b �� �F�n�_i�̐���l
�s ���� �F�n�_i�ƒ����n�_j�̋����̋t���i�P�^�q�����j
�b ���F�����n�_j�̒l
p �F�ׂ���W��
| �i�Q�l�j | ��Ԗ@�ɂ��ẮA�����@���i���s��w�H�w���j��́u�����ϑ��_�̓K���z�u�Ɋւ���V�X�e����́v�i������������������ 48���j�A�吼�s�Y�i�������������j�����s��w�h�Ќ������ɂ����Ă���킵���u�X�v���C���@��p�����Q������Ԃɂ��āv�iJ.Oceanogr. Soc.Jpn 31�j�Ȃǂɔ�r�I�ڂ�����@�̐������Ȃ���Ă���B |
�@�Ƃ���ŁA�q��@�����̐���ɏ�L�̕�Ԗ@��p�����œ�̉ۑ肪����B
�@��͏]���̕�Ԗ@�́A����n�_�̒l(C)�͂��̔���������̋���(R)�ɋt��Ⴕ�ď������Ȃ�Ƃ��������Ɋ�Â��Ă��邽�߁A�ʏ�A��C�Z�x�␅���Z�x�̏ꍇ�ɂ́Ap�̒l���P����T�ɂ����Ă��̏��������������B�������A�������x���ɂ����ẮAp�̒l������ɂ�����炸�l(C)������(R)�ɒP���ɋt��Ⴗ��Ƃ������������藧���Ȃ����Ƃ�����B
�@�܂�A�q��@�������x���̏ꍇ�ɂ́A�������x���̒l(P)�Ƌ����iSD:�q��@�ƌv���l�̍ŒZ�����j�Ƃ̊Ԃɂ́A�ΐ��i���K���Y���j������W�����邱�Ƃ��m���Ă���A��L�ׂ̂����ԁA���z����ԁA�X�v���C����Ԃɂ͂Ȃ��܂Ȃ����Ƃ��m���Ă���B
�@������̏]���̎�@���q��@�����ɓK�p�����ł̉ۑ�́A�]���̕�Ԗ@�́A�����≌���Ȃǂ̔��������A�Œ蔭�����Ȃ��������������L�����ĕ��ω����ꂽ��Ԃɂ���ꍇ�ɗL���ł��邱�ƂɋN�����Ă���B
�@���Ȃ킿�A�q��@�����⎩���ԁA�S���Ȃǂ̈ړ��������i�������Ȃ����A���_�����j�ł́A�v�����������K�͂łȂ��ƁA��Ԍ��ʂ��Ȃ߂炩�ɕ��������ꂸ�A�����v���l���������n�_�𒆐S�ɁA�������̓��ٓ_�i������h�ڋʁh�j���ł��Ă��܂����ƂɂȂ�A�\���ȕ�Ԍ��ʂ������Ȃ����Ƃ��w�E����Ă���B
�@������C�ۑS�nj�ʌ��Q�Ɗ������ �������������́A�����̒n�_�ɂ�����q��@�����̃s�[�N���x���̎����l�����`���Ӓn��S�̂̑������x���̍L����𐄒肷�邽�߂̐V��@�������J�����Ă����B
�@�V��@�̓����́A�]���̕�Ԗ@�̉ۑ�A���Ȃ킿�q��@�̑������x���Ǝ_�Ƃ̋����Ƃ̊W�ɂ������ۑ�y�шړ������ւ̑Ή��ɂ������ۑ���ɉ�������ƂƂ��ɁA�]���̎�@�ł͍������Ă��������l�����Ƃɂ��������\�����\�Ƃ��邱�Ƃɂ���B
�@�V��@�̌����́A�ȉ��̂Ƃ���ł���B
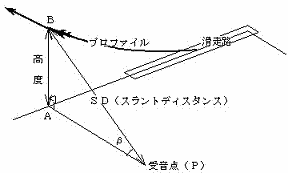
�@�q��@�������x��(L)�́A�_(P)�Ƃ̍ŒZ�����iSD:�X�����g�f�B�X�^���X�Ƃ����A�}�P�|�P�Q�Ɓj�Ƃ̊Ԃɂ́A�����f�[�^�̓��v��͂���ΐ��i���K���Y���j��������̎�1-2�̊W�����邱�Ƃ��m���Ă���B
�k���`�Elog(�r�c�^50) �Q�{�a�Elog(�r�c�^50)�{�b............................��1-2
�������A
�k�@�@�@�@�F�_�i�o�j�ɂ�����q��@�̑������x���i�ʏ�A�s�[�N���x���j(dB(A))
�r�c �@�@�F�q��@�̔�s�o�H�ƒ����n�_�����ԍŒZ�����@(m)
�`�A�a�A�b�F�ŏ��Q��@�ɂ����Ƃ߂���A�W��
�i�Q�l�j �q��@�������x���ƃX�����g�f�B�X�^���X(SD)�Ƃ̊W�ɂ��Ă̌����́A���䏹�K�i�����H�Ƒ�w�H�w���j��́u�����\���]����@�����v�i���a56�N3���j�y�уA�����J�A�M�q���(FAA)�Ȃǂ̌���������B
�@��1-2�̊W�́A�����f�[�^�i�}�P�|�Q�Ɏ������n�_�ɂ����đ���j���ŏ����@�ɂ���A���́i���v���́j���邱�Ƃɂ���ē����邪�A�q��@�������x���ƃX�����g�f�B�X�^���X�̊W���i���ۂɂ͌W���j�́A�@�했�A���������ɈقȂ邾���łȂ��A�q��@�̔�s�v���t�@�C���ɂ���Ă��قȂ�B
�@���������āA�����ɂ���ĕ����̒����n�_�ɂ����ċ@��ʁA�������ʁA�v���t�@�C���ʂɁA�q��@�����̃s�[�N���x���y�уv���t�@�C������l��������������A����v��͂��邱�Ƃɂ��A�@��ʁA�������ʁA�v���t�@�C���ʂ̌W��(A, B, C)�������A���ʂƂ��ĔC�ӂ̃X�����g�f�B�X�^���X�ɂ�����q��@�������x��������\�ƂȂ�B
�}�P�|�P �@�q��@��������ɂ�����X�����g�f�B�X�^���X(SD)
 �@
�@
�}�P�|�Q �����n�_�i�h�� ���j
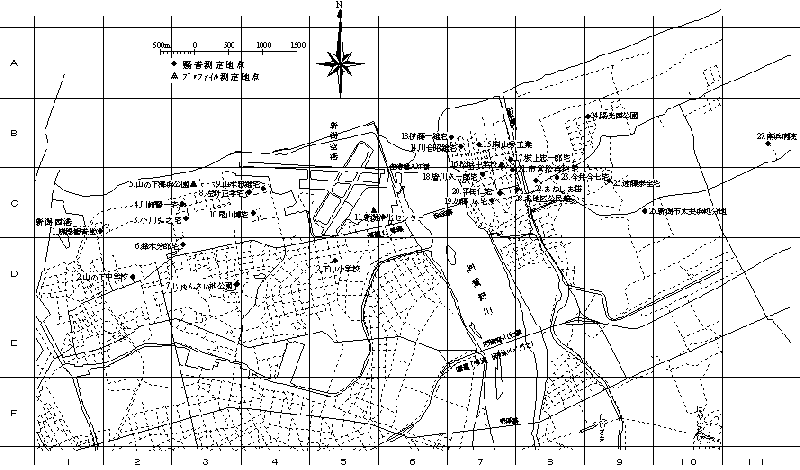
�@���̐V��@�̏ꍇ�A�C�ӂ̒n�_�ɂ�����X�����g�f�B�X�^���X���K�v�Ȃ��Ƃ���A�q��@�̃v���t�@�C���i��s�o�H���p�A���ʁj���������f�[�^�����邱�Ƃ��s���ƂȂ�B�i�v���t�@�C���v���̕��@�Ƃ��̑��u�ɂ��ẮA�ʓr�A�v���t�@�C�������̍����Q�Ƃ̂��ƁB�j
�B ���b�V����̔C�Ӓn�_�̃s�[�N���x���Z�o�ւ̊�b�����̉��p
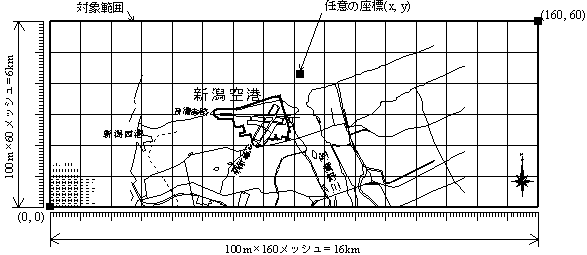
�@����ł͓�k16km�A����6km���Ώ۔͈͂Ƃ��A�P���b�V���̑傫����100m�~100m�Ƃ��ē�k������60�A����������160�̃��b�V����ݒ肵���B�i�}�P�|�S�j
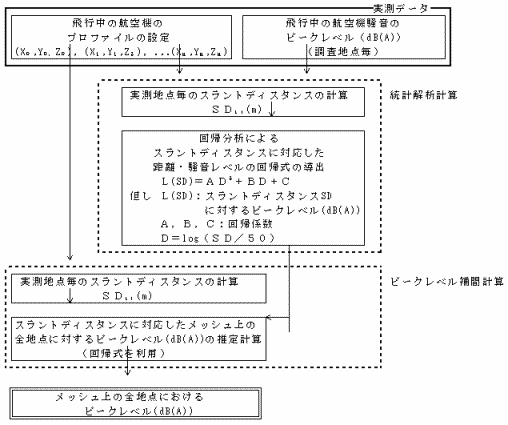
�@���̒����Ώ۔͈͓��̕����̒����n�_�ɂ�����q��@�������x�������f�[�^�A�v���t�@�C������f�[�^�Ȃǂ�p���āA�Ώ۔͈͓��̃��b�V����̔C�ӂ̒n�_�ɂ�����s�[�N�������x�����Z�o����菇��}�P�|�R�Ɏ����B
�@�Ȃ��A�{��@�ł͓��v��͂��s����ŁA���Ȃ��Ƃ�10�n�_�ȏ�̎����n�_����`���ӂɕK�v�ƂȂ�B����ł͂��̌����ɂ����đ���n�_�i25�n�_�j��ݒ肵���B�i����n�_�̈ʒu�ɂ��Ă͎Q�l�����̐}�P�|�Q���Q�Ɓj
�}�P�|�R�@��`���ӂ̔C�ӂ̒n�_�i���b�V����̑S�n�_�j�ɂ�����s�[�N���x���𐄒肷��菇
�}�P�|�S�@�����Ώ۔͈͂ɂ����郁�b�V�����W�̐ݒ�
�@�}�P�|�R�Ɏ�������Ԍv�Z��@�ɂ��A�����Ώ۔͈͓��̃��b�V����̑S�Ă̒n�_�ɂ�����q��@�����̃s�[�N�������x���l�𐄒肷�邱�Ƃ��ł���B
�@�P���̂��ׂĂ̕ւɂ��Ă��̎�@��p���ăs�[�N�������x���̕�Ԍv�Z�����{���A���b�V����̒n�_���Ƃɂ����̃s�[�N�������x���̃p���[���ς��Z�o���邱�Ƃɂ��AWECPNL�ɂ����������̍������i��1-3�j��K�p���āA���b�V����̑S�n�_�ɂ�����WECPNL���v�Z���邱�Ƃ��o����B�i�}�P�|�T�A�}�P�|�U�j
����������
|
...................��1-3 |
|
��s�� |
���ԑ� |
���� |
|
�m �P |
�� |
0:00 - 7:00 |
|
�m �Q |
�� |
7:00 - 19:00 |
|
�m �R |
�[ |
19:00 - 22:00 |
|
�m �S |
�� |
22:00 - 24:00 |
|
|||
| �� �� �� �� �� �� �� �� �� �� �� |
�s�����������t WECPNL �������k�`�����{�P�Olog�m�|�Q�V �m���m �Q�{�R�m�R�{�P�O�i�m�P�{�m�S�j �Y����, ��: ���b�V����̂��C�����W�i�P���b�V��100m�j
|
||
|
|||
�@�}�P�|�U�@���b�V����̑S�n�_�ɂ�����WECPNL�Z�o�̊T�O�}
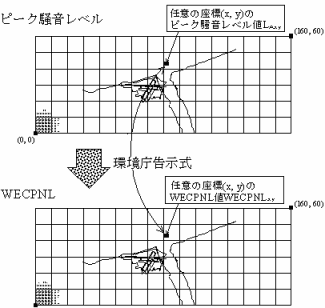
�@�C�ł͂P���P�ʂ�WECPNL���Z�o���邽�߂̍l���������������A�����Č����s���ɂ́A�N���σ��x����WECPNL���Z�o����K�v������B���̂��߂ɂ́A�������{�N���̕��ϓI�ȋ�`�g�p�i���ԑѕʂ̕��A�@��ʕ��A�����H�g�p�����Ȃǁj�̎��уf�[�^����ɔN�ԕ��ς̃s�[�N�������x���l�����߂�K�v������B
�@�q��@�������x���̑傫���́A�q��@�̔�s�o�H�A���x�A�@��A�������̕ʁA�����A�����A�V�̋C�ۏ������A�n�`�E�y�n���p���̒n�\�ʂ̏����Ȃǎ�X�̗v���ɂ���ĈقȂ�B�����Ŗ{��@�ł́A���������ɂ�钼�ڒ������ʈȊO�ɁA�ȉ��Ɏ������ڂ��������Đ��肷�邱�ƂƂ����B
(�A) �N�Ԃ̕��ϓI�ȃt���C�g�X�P�W���[���i�@��ʁA�����n�ʁA���ԑѕʁj
(�C) �����H�g�p�����̔N�Ԏ��сi�@��ʁA�����n�ʁj
(�E) �N�Ԃ�ʂ��������̏o���p�x�i�����H�g�p�����̎��уf�[�^�������Ȃ��ꍇ�j
(�G) �n���I�ȗv���ɂ��q��@�������x���̉e���̕�i�����l���ɂ��j
�@���ۂɂ́A�s��E�@��E�������E�����H���p�������̔N�ԏo�����ɁA�ތ^��������s�o�H�i�Q�l���� �}�Q�|�S �j�̏o���p�x���l���������i�Q�l���� �\�Q�|�R�j��p���āA�s�[�N���x���̎����l���o���p�x�ʼn��d�i�p���[�j���ρi��1-4�j���邱�Ƃɂ��A�N�ԕ��ς̃s�[�N���x���̃p���[���ϒl���Z�o����B
�k �`��10�~log10 �i���v���~10�kAi/10�j...................................��1-4
�k �` :�P���̂��ׂẴs�[�N���x���̃p���[���ϒl
�k �`��:�s��E�@��E�������E�����H���p�����ʂ̕��σs�[�N���x��
�v �� :�s��E�@��E�������E�����H���p�����ʂ̏o������
�@���̃p���[���ϒl�Ǝ��ԑѕʂ̔N�ԕ��ϕ��������������i��1-3�j�ɓK�p���A�N�Ԃ̕��ϓI��WECPNL���Z�o����B
�@�����\���̎�@�ɂ��Ă��A�����Č��̏ꍇ�Ɠ��l�ɍl���邱�Ƃ��ł���B
�@�����N���ɂ�����̔N�ԕ��ϓI�ȃt���C�g�X�P�W���[���́A�P��������̕��A�������̎��ԑѕʂ̕��A�@��A�ꍇ�ɂ���Ă͊����H���������قȂ�B
�@�����ɂ�����@��ʁE���ԑѕʂ̏o���������A����̎��уf�[�^�ɒu�������A�D�Ɠ��l�ɏ����̏o���p�x���Z�o���A���̌�͌���Ɠ��l�Ɏ�1-4��p���ĔN�ԕ��ς�WECPNL�l���v�Z����B
�@�������A�����N���ɂ����Ċ����H�̉����A�V�݂��\�肳��Ă���ꍇ�A���s�@��ƈقȂ�@�킪�������ꂽ�ꍇ�ɂ͂����̏����ɂ��Ă��A�{��@�ł̓v���t�@�C���f�[�^�̏C���A����`�ɂ���������f�[�^���Q�Ƃ���Ȃǂɂ���čl�����邱�Ƃ��\�ł���B
�@�q��@�����̓��������i�ȉ��u�R���^�[�v�Ƃ����j�́A��ɎZ�o�������b�V���P�ʂ̔N����WECPNL�l�i����Č��l���邢�͏����\���l�j�����ƂɁA���z����Ԗ@��p����75�A70�Ƃ�����WECPNL�̒l�������W�����X�ɐ��Ō���ł䂭���Ƃɂ��쐬���邱�Ƃ��ł���B
�@�{��@�ł͑S�̂̌v�Z�����Ȃ������ƂȂ��C�ӂ�WECPNL�l�̃R���^�[���쐬���邱�Ƃ��o����B
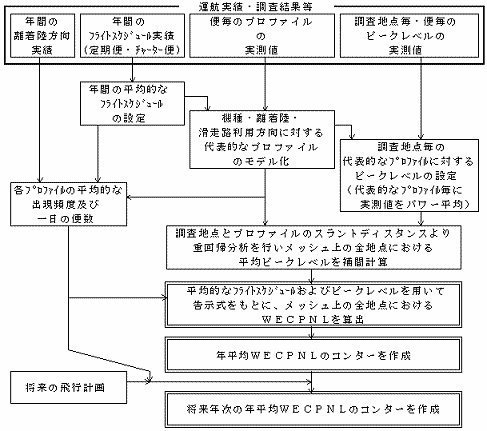
�@����܂ŁA�V��@�̊�b�������q�ׂĂ������A������S�̂Ƃ��Ă܂Ƃ߂��̂��A�}�P�|�V�ł���B�}�̏�i�́A���Ԓ����ɂ��f�[�^�̎��W���A���i�͌����Č����x���ɂ�����N����WECPNL�R���^�[�̍쐬�̎菇���A���i�͑��֓��̏�����s�v��ɑΉ������N���Ϗ���WECPNL�R���^�[�쐬�̎菇�����ꂼ�ꎦ�������̂ł���B
�}�P�|�V WECPNL�N���σR���^�[�̍쐬�菇�i���g���͎����f�[�^�j
�@�V��@�́A�����f�[�^�����ƂɌ���ɂ������`���ӂ�WECPNL�𐄒肷��s�����Č��t�ƁA���ցA�����H�������̏����v��ɑΉ������s�����\���t�̗����Ɏg���邱�Ƃ��傫�ȓ����ƂȂ��Ă���B��@�Ƃ��Ă̓����͎�Ɏ��̂T�ł���B
(�A) �e�����n�_�̎����f�[�^�������Č��Ə����\���ɍő���������Ă��邱��
(�C) �N���ς̉^�q���сE�\������ڍׂɔ��f�ł��邱��
(�E) ���ցA�@��ύX�A�����H�����ȂǑO��������ω����Ă������\�����\�Ȃ���
(�G) �ꕔ�̕ւ���s�o�H��ύX�����Ƃ��Ă������\���ւ̑Ή����\�Ȃ���
(�I) �q�ϓI�ȃf�[�^�ɂ̂݊�Â��Ă���̂ōČ�������������
�@�ȏ�̗\�������Ɋ�Â�������@�ɑ��āA�]�茸���̍l���A�n���I�������l�����邽�߁A�ȉ��Ɏ������ǂ��s�����B
�@��s�o�H�������痣�ꂽ�n�_�ɂ����ẮA�}�P�|�W�Ɏ�����SD�Ƒ������x���̊W�i���������Ƒ�C�z���ɂ�錸�����l���j�ȊO�ɁA�]�茸�����l������K�v������B
�@�]�茸���Ƃ��Ă��@�̂ɂ��Օ������i�@�̎��g�ɂ���ăG���W�����Օ�����A�������x��������������ʁj�ƁA�n��`�������i�n�\�ʂɂ�鑛�����x���̌������ʁj���l�������B
�@�@�̎Օ��ɂ��Օ�������LEB�́A�ϑ��_����@�̂����グ���Ƃ��̋p���̊��Ƃ��Ď�����Ă���B�i��1-5�A�����\���]����@�����A���a56�N3���A�����H�Ƒ�w�j
LEB=3(1- sin�� ) 10��<��<90��
LEB=0 ��>90��
��1-5
�}�P�|�W�@�@�̎Օ��ɂ�錸��
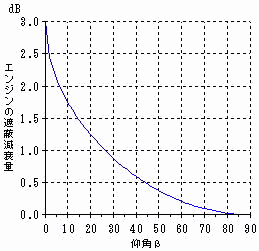
�@�n�\�ʂɂ�錸���ʂ͊ϑ��_����q��@�܂ł̐�������l�Ƌp���̊��Ƃ��Ď�����Ă���B�i��1-6�A�č������ԍH�Ɖ�(SAE)�j
��(��, l )=G(l)�~��(��)/13.86
��1-6 ������ G(l)=15.09[1-��-2.74�~10 �|�R l ]
G(l)=13.860��l��914m
l��914m��(��)=3.96-0.066��+9.9��-0.13��
��(��)=0 60��0��������60��
������90��
�}�P�|�X�@�n�\�ʂɂ�錸���@

�@�ȏ�̗]�茸�����l�����Ď����l�����A�W�����Z�o����ꍇ�ɂ́A�����������x���ɁA�e�����n�_�Ɣ�s�o�H�̊W����Z�o�����]�茸���������炩���߉��Z���Ă���A��A�W���̎Z�o���s���B
�@���̌�Z�o������A�W����p���ĎZ�o�����������x������]�茸�������������Ȃ���Ȃ�Ȃ��B
�@�ȏ�̉��ǂ��������ꍇ�ł��A�����l�Ɖ�A���ɂ�鐄�v�l�̊Ԃɂ͈Ⴂ��������B���̎�ȗv���Ƃ��Ă͈ȉ��̂��Ƃ��l������B
�@�ȏ�̏����̈Ⴂ���ʂɍl�����邱�Ƃ͍���Ȃ��߁A�����ł͎����n�_�ɂ������A���ɂ�鐄�v�l�Ǝ����l�̍��̒n���I�ȕ��z���l�����邱�ƂƂ���B�n���I�ȕ��z�ւ̕�Ԏ�@�Ƃ��Ă̓X�v���C����Ԗ@����p���邱�Ƃ��l������B�i���̎�@�ɂ��Ă͊J�����Ȃ̂ŏڍׂ͂����ł͎����Ȃ��B�j
�@�������A���v�l�Ǝ����l�̍���P�ɕ�Ԃ���ȑO�̒i�K�ŁA��A���ɂ�鐄�v�l��������Č��ł��Ă��邱�Ƃ��A�����f�[�^�A��A�W���A���v�f�[�^���\���Ɋm�F���A���������錴���͂��ă��f���̉��ǂ��s���K�v������B���̌�ɒn���I�ȕ��z�����m�F���Ȃ����Ԃ��s��Ȃ���Ȃ�Ȃ��B
������� ������������
��152-0033 �����s�ڍ���剪�R1-31-9-401
TEL 03-6421-4610, FAX 03-6421-4611
�A���惁�[���A�h���X�F office@eritokyo.jp
(C)Copyright by ![]()
�@�{�z�[���y�[�W�̓��e�̕����A�]�ڂ��ւ��܂��B�܂��{�z�[���y�[�W�̒��쌠�͊������ �������������ɂ���܂��B